
Back إسقاط تشكيلي Arabic Transformació conforme Catalan Konformní zobrazení Czech Konforme Abbildung German Conformal map English Konforma bildigo Esperanto Transformación conforme Spanish نگاشت همدیس Persian Konformikuvaus Finnish העתקה קונפורמית HE
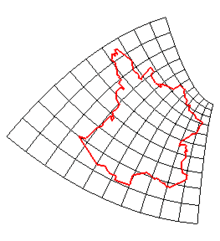

En mathématiques, et plus précisément en géométrie et en analyse complexe, une transformation conforme est une bijection qui conserve localement les angles, c'est-à-dire qui se comporte au voisinage de chaque point où elle est définie presque comme une similitude.
Dans le plan, les transformations conformes qui conservent les angles orientés ont une telle utilité qu'il est fréquent[1] qu'elles soient les seules baptisées du terme de conformes. Elles se confondent alors avec les bijections holomorphes. Les transformations conformes indirectes sont, dans ce cas, appelées transformations anticonformes.
On rencontre les transformations conformes en géométrie différentielle, dans des problèmes d'électrostatique ou dans la résolution de l'équation de Poisson[2], en mécanique des fluides pour modéliser des écoulements, et en cartographie.
La notion de transformation conforme se généralise à des espaces de dimension supérieure à 2, mais elle y perd un peu de sa diversité.
- Cet usage est fréquent (voir par exemple ce cours de l'Ensem p.10) mais pas universel (voir ce cours de l'umc ou bien Marcel Berger, Géométrie [détail des éditions], t. 2, p. 93).
- Jacques Harthong, « Cours d'analyse mathématique », , p. 121.